Karar Ağaçları & ID3 Algoritması
01/03/2025Makine öğrenmesi ve veri madenciliği dünyasında karar ağaçları, hem anlaşılması kolay hem de güçlü sonuçlar sunan denetimli öğrenme yöntemlerinden biridir. 1960’lı yıllardan itibaren veri analizi ve yapay zeka çalışmalarının önemli bir parçası olmuştur. Her düğümde verinin belirli bir özelliğe göre ayrıldığı ağaç yapıları oluşturarak karmaşık karar verme süreçlerini basit ve anlaşılır parçalara böler. Böylece ağaç yapıları görselleştirilerek nasıl ve neden belirli sonuçlara ulaşıldığını yorumlamak kolaylaşır.
Karar ağaçlarının kullanım alanları geniş bir yelpazeden oluşur. Finanstan sağlığa, pazarlamadan eğitime birçok farklı sektörde, kredi risk analizi, dolandırıcılık tespiti, klinik verilerin analizi, satış tahminleri, ürün öneri sistemleri gibi çözümleri hayata geçirmek için kullanılabilir.
Bir karar ağacı oluşturmak için kullanılabilecek farklı algoritmalar mevcuttur. Kullanılan algoritmaya bağlı olarak sınıflandırma veya regresyon problemlerinde çözüme ulaşmak mümkündür. Yaygın olarak kullanılan bazı algoritmalar:
- • ID3 (Iterative Dichotomiser 3) Algoritması:
En temel karar ağacı algoritmasıdır.
Bilgi kazancı (information gain) metriğini kullanır.
Sürekli verilerle doğrudan çalışamaz, verilerin kategorik hale getirilmesi gerekir.
Aşırı öğrenme riski yüksektir. - • C4.5 Algoritması:
ID3 algoritmasının geliştirilmiş versiyonudur.
Bilgi kazancı yerine kazanç oranı (gain ratio) metriğini kullanır.
Sürekli verilerle çalışabilir.
Aşırı öğrenme riskini ortadan kaldırmak için gereksiz dalların temizlendiği bir mekanizmaya sahiptir. - • CART (Classification and Regression Trees):
Gini indeksi metriğini kullanır ve hem sınıflandırma hem de regresyon problemlerinde kullanılabilir.
Karar ağacını ikili bölme ile oluşturur yani her düğümde sadece iki dal bulunur. - • CHAID (Chi-Square Automatic Interaction Detection):
Ki-kare testi kullanarak değişkenler arasındaki bağımlılığı analiz eden bir algoritmadır.
Kategorik veri analizinde güçlüdür.
Pazarlama ve sosyal bilimler gibi alanlarda yaygın olarak kullanılır.
Biz bu yazıda ID3 algoritması ile bir karar ağacı oluşturmanın üzerinde duracağız.
ID3 Algoritmasının Çalışma Prensibi
ID3 algoritmasının karar ağaçlarının düğümlerini seçerken bilgi kazancı metriğini kullandığını söylemiştik. Hedef değişken dışındaki her bir değişken için bilgi kazancı, hedef değişkenin entropisi ile ilgili değişkenin hedef değişkene göre entropisinin farkıyla elde edilir.
$c$ değişkenin farklı değerlerinin sayısı, $p_i$ her değerin frekansı olmak üzere entropi aşağıdaki denklemle hesaplanır:
Basit bir örnek üzerinde göstermek gerekirse, $F1$ ve $F2$ özellikler, $L$ hedef değişken olacak şekilde hedef değişkenin entropisi aşağıdaki gibi bulunur:
| F1 | f2 | L |
|---|---|---|
| x | a | t |
| x | b | t |
| x | b | f |
| y | b | f |
| y | b | f |
Bir değişkenin hedef değişkene göre entropisi hesaplanırken, ilgili değişkenin birbirinden farklı her değerinin frekansı, bu değere karşılık gelen hedef değişken değerlerinin sayısına göre hesaplanan entropi ile çarpılır ve tüm çarpımlar toplanır.
$F1$ değişkeni için x değerlerinin frekansı $3/5$, bu x değerlerinin olduğu satırlarda hedef değişken değerlerinden biri f, ikisi t değerine sahip. y değerlerinin frekansı ise $2/5$ ve bu iki satırın ikisinde de hedef değişken değeri f. Bu değerlere göre $F1$ ve $F2$ değişkenlerinin hedef değişkene göre entropileri ve bilgi kazançları aşağıdaki gibi hesaplanır.
Çalışma Adımları:
- Hedef değişken entropisi hesaplanır.
- Diğer değişkenlerin koşullu entropileri ve bilgi kazançları hesaplanır.
- En yüksek bilgi kazancına sahip özellik düğüm olarak seçilir.
- Seçilen özelliğin değerlerine göre tablo parçalara ayrılır.
Bu işlemler tablonun ayrılan her parçası için tekrar edilir. Sonunda hedef değişken için hesaplanan entropi 0 olduğunda, ayrılmış olan tabloda hedef değişkenin tüm değerleri aynı demektir. Bu da karar ağacının bir ucuna (yaprak düğüme) ulaştığımız anlamına gelir.
Bunu bir örnekle pekiştirelim. Aşağıdaki tabloda kan şekeri, vücut kitle indeksi, yaş ve ailede diyabet öyküsü değişkenlerine göre verilmiş diyabet riski verileri bulunuyor. Hangi değişkenin diyabet riski üzerinde ne kadar etkili olduğundan hareketle bizi diyabet riski sonuçlarına götüren bir karar ağacı oluşturalım.
| Kan Şekeri | Vücut Kitle İndeksi | Yaş | Ailede Diyabet öyküsü | Diyabet Riski |
|---|---|---|---|---|
| yüksek | normal | genç | var | yüksek |
| düşük | kilolu | genç | yok | düşük |
| çok yüksek | obez | genç | yok | yüksek |
| normal | zayıf | genç | var | düşük |
| yüksek | kilolu | orta yaşlı | var | yüksek |
| normal | normal | orta yaşlı | var | düşük |
| normal | kilolu | orta yaşlı | var | yüksek |
| çok yüksek | normal | yaşlı | yok | yüksek |
| çok yüksek | normal | orta yaşlı | var | yüksek |
| normal | normal | genç | var | düşük |
| düşük | zayıf | orta yaşlı | var | yüksek |
| normal | zayıf | orta yaşlı | yok | düşük |
| düşük | normal | yaşlı | yok | düşük |
| yüksek | kilolu | genç | yok | düşük |
| çok yüksek | kilolu | genç | var | yüksek |
| yüksek | normal | genç | yok | düşük |
| düşük | zayıf | yaşlı | yok | düşük |
| normal | kilolu | yaşlı | yok | yüksek |
| çok yüksek | kilolu | orta yaşlı | yok | yüksek |
| düşük | kilolu | yaşlı | var | yüksek |
| normal | normal | yaşlı | yok | düşük |
| yüksek | normal | yaşlı | yok | yüksek |
| yüksek | normal | yaşlı | var | yüksek |
| yüksek | obez | orta yaşlı | var | yüksek |
| normal | obez | genç | var | yüksek |
Diyabet riski değişkeni 15 yüksek, 10 düşük değerine sahip, hedef değişken entropisi:
Diğer değişkenlerin hedef değişkene göre entropileri ve bilgi kazançları:
Kan şekeri en yüksek bilgi kazancı değerine sahip değişken, kök düğüm olarak seçilir ve tablo buna göre parçalara ayırılır.
| Kan Şekeri | Vücut Kitle İndeksi | Yaş | Ailede Diyabet Öyküsü | Diyabet Riski |
|---|---|---|---|---|
| çok yüksek | obez | genç | yok | yüksek |
| çok yüksek | kilolu | genç | var | yüksek |
| çok yüksek | normal | orta yaşlı | var | yüksek |
| çok yüksek | kilolu | orta yaşlı | yok | yüksek |
| çok yüksek | normal | yaşlı | yok | yüksek |
| Kan Şekeri | Vücut Kitle İndeksi | Yaş | Ailede Diyabet Öyküsü | Diyabet Riski |
|---|---|---|---|---|
| yüksek | normal | genç | yok | düşük |
| yüksek | normal | genç | var | yüksek |
| yüksek | obez | orta yaşlı | var | yüksek |
| yüksek | kilolu | genç | yok | düşük |
| yüksek | kilolu | orta yaşlı | var | yüksek |
| yüksek | normal | yaşlı | yok | yüksek |
| yüksek | normal | yaşlı | var | yüksek |
| Kan Şekeri | Vücut Kitle İndeksi | Yaş | Ailede Diyabet Öyküsü | Diyabet Riski |
|---|---|---|---|---|
| normal | zayıf | genç | var | düşük |
| normal | zayıf | orta yaşlı | yok | düşük |
| normal | obez | genç | var | yüksek |
| normal | normal | orta yaşlı | var | düşük |
| normal | kilolu | yaşlı | yok | yüksek |
| normal | kilolu | orta yaşlı | var | yüksek |
| normal | normal | genç | var | düşük |
| normal | normal | yaşlı | yok | düşük |
| Kan Şekeri | Vücut Kitle İndeksi | Yaş | Ailede Diyabet Öyküsü | Diyabet Riski |
|---|---|---|---|---|
| düşük | kilolu | genç | yok | düşük |
| düşük | zayıf | orta yaşlı | var | yüksek |
| düşük | zayıf | yaşlı | yok | düşük |
| düşük | normal | yaşlı | yok | düşük |
| düşük | kilolu | yaşlı | var | yüksek |
Kan şekeri değişkeninin her değeri için oluşturulan alt tablolarda kan şekeri dışında kalan sütunlar için hesaplamalara devam edilir. Kan şekeri değişkeninin düşük değerini gösteren alt tablo için entopi ve bilgi kazancı değerleri:
Ailede diyabet öyküsü değişkeninin bilgi kazancı en yüksek olduğu için kan şekerinin düşük değerinin altına ailede diyabet öyküsü değişkeni getirilir.
Tablo parçalara ayrıldıkça aynı işlemleri her alt tablo için tekrar ederek nihayetinde bir karar ağacı yapısına ulaşırız.
Bir yaprak düğüme nasıl ulaşıldığı konusuna örnek olması için kan şekeri değişkeninin çok yüksek değeri için ayrılan tabloya bakabiliriz. Aşağıda görüleceği üzere bu alt tabloda hedef değişken entropisini hesapladığımızda 0 sonucuna ulaşırız. Bunun sebebi diyabet riski değişkeninin bu tablodaki bütün değerlerinin birbiriyle aynı olmasıdır.
Örnek veri setine göre tüm hesaplamalar yapıldığında karar ağacı aşağıdaki şeklini alır.
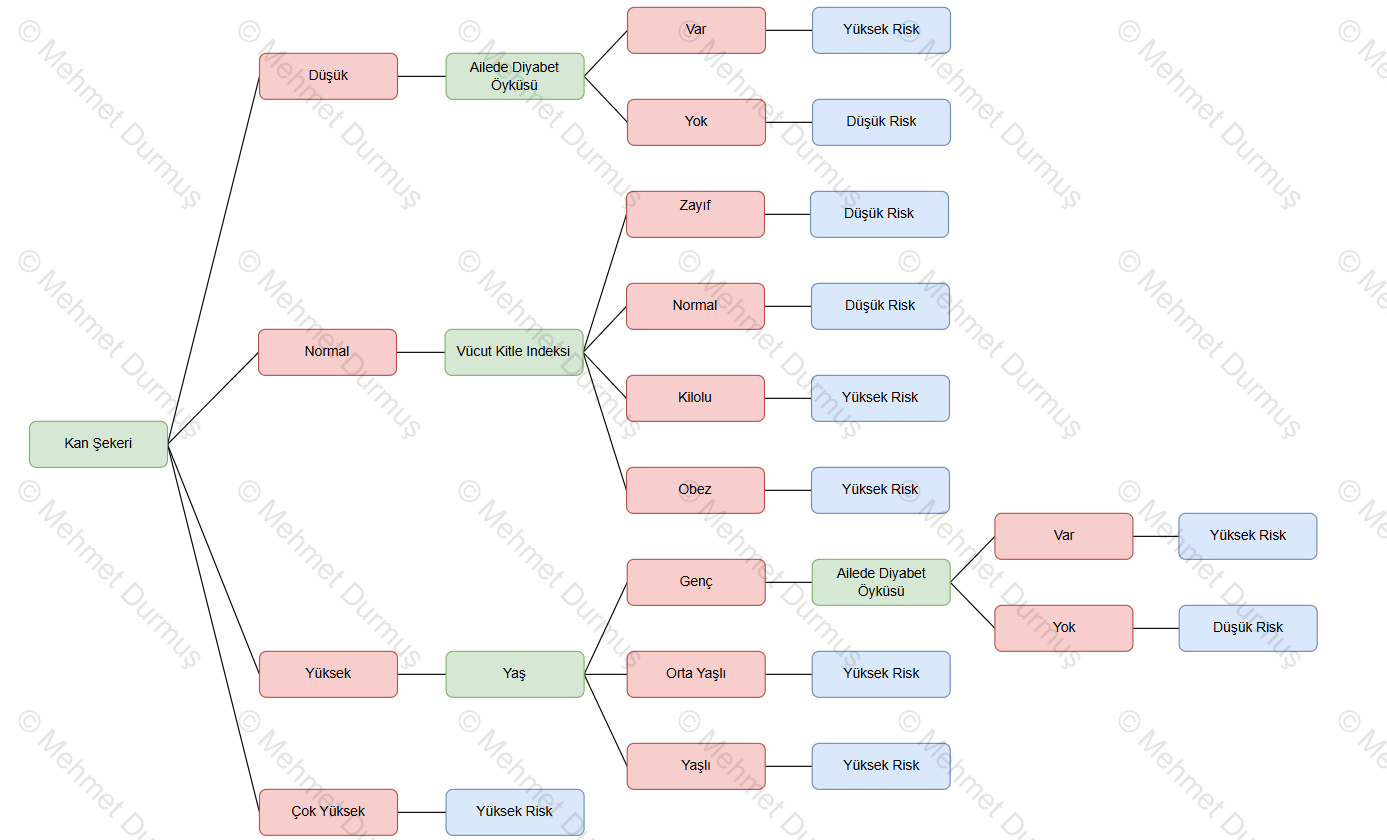
Bu yazıda entropi, bilgi kazancı gibi matematiksel kavramların karar ağacı modellerinin arkasındaki teoriyi nasıl desteklediğini ve bu yaklaşımın pratik veri analizinde nasıl somut örneklere dönüştüğünü inceledik. ID3 algoritmasının veriyi nasıl yapılandırıp anlamlandırabileceğimizi ortaya koyduğu bu sürecin sizlere de ilham verdiğini umuyorum.